



Next: 1. Introduction
Up: thesis
Previous: List of Tables
- 1.1. A physical interpretation of the underlying coupling in the Kondo
model.
- 1.2. A physical depiction of the the Hubbard model allowing for electrons to
hop with transfer integral
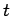 and experience a local Coulomb repulsion
and experience a local Coulomb repulsion 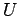 .
.
- . The dimensionless effective hybridization function
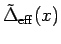 evaluated for
evaluated for
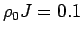 in the SIKM. The resulting function is symmetric and is only plotted for
in the SIKM. The resulting function is symmetric and is only plotted for
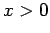 . It coincides with the universal form for
. It coincides with the universal form for
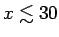 .
The dashed line represents the fit
(2.14) and is nearly indistinguishable from the actual data.
Notice especially the appearance of logarithmic behavior in the
crossover region.
.
The dashed line represents the fit
(2.14) and is nearly indistinguishable from the actual data.
Notice especially the appearance of logarithmic behavior in the
crossover region.
- 2.2. Universal curve for
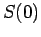 as function of the local magnetic field
as function of the local magnetic field
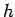 .
.
- 2.3.
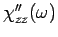 for three characteristic local magnetic fields
for three characteristic local magnetic fields
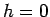 ,
,
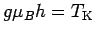 and
and
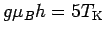 .
.
- 2.4. The magnetic susceptibility
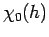 from equ. (2.23) (circles)
and the same quantity obtained from an NRG calculation.
from equ. (2.23) (circles)
and the same quantity obtained from an NRG calculation.
- 2.5. Results for the Shiba ratio
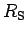 (full line) and
the Wilson ratio
(full line) and
the Wilson ratio 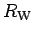 (dashed line) as a function of a local magnetic
field. The
correct limiting values at
(dashed line) as a function of a local magnetic
field. The
correct limiting values at 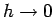 are missed by approximately 5%.
are missed by approximately 5%.
- 3.1. In the DMFA all electron propagators are averaged over the
entire Brillouin Zone (BZ); effectively mapping the lattice onto a
single point (top). In the DCA, we break the BZ into several
sub-cells which are now in turn averaged over mapping the lattice
onto a finite sized cluster (bottom).
- 3.2. Self-consistency loop for the DCA.
- 3.3. Diagrams relating the self-energy to the reducible
two-particle longitudinal spin and charge (top) and transverse
spin (middle) vertices. A similar relation is obtained for the
particle-particle channel (bottom).
- 3.4. Bethe-Salpeter equation relating the reducible two-particle vertex
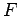 to the
irreducible vertex function
to the
irreducible vertex function 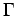 .
.
- 3.5. Flow chart for the Ansatz self-consistent implementation of the MSMB/DCA.
- . Second order diagrams for the vertex functions
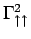 - a.) and
- a.) and
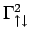 - b.) for an external momentum
transfer
- b.) for an external momentum
transfer 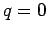 .
.
- 3.7. Imaginary part of the self-energy at lowest Matsubara frequency as obtained by various
cluster solvers and FLEX/MSMB method at
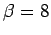 ,
, 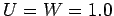 , and
, and 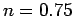 .
The MSMB cluster sizes are
.
The MSMB cluster sizes are
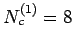 and
and
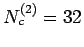 .
.
- 3.8. Flow chart depicting two independent self-consistent DCA calculations combined
via an Ansatz to construct a MSMB self-energy.
- 3.9. Imaginary part of the self-energy at lowest Matsubara
frequency as obtained by the MSMB method using first (FLEX) and
second order approximated irreducible vertices
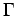 in
comparison to the large single-cluster QMC results at
in
comparison to the large single-cluster QMC results at 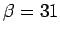 ,
,
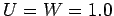 , and
, and 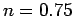 . Multi-scale results are for cluster sizes
. Multi-scale results are for cluster sizes
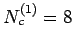 and
and
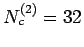 .
.
- 3.10. Imaginary part of the
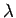 -approximated self-energy at
lowest Matsubara frequency for the large cluster (
-approximated self-energy at
lowest Matsubara frequency for the large cluster (
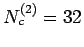 )
using various cluster solvers in comparison to the single cluster
QMC result at
)
using various cluster solvers in comparison to the single cluster
QMC result at 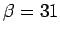 ,
, 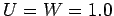 , and
, and 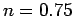 . Also shown is the
overestimated Ansatz self-consistent self-energy of the MSMB
method for the second order approximated
. Also shown is the
overestimated Ansatz self-consistent self-energy of the MSMB
method for the second order approximated 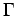 .
.
- 3.11. Imaginary part of the self-energy at lowest Matsubara
frequency as obtained by the MSMB approach using the second order
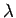 -approximation and large single-cluster QMC. Results are
for various small cluster sizes
-approximation and large single-cluster QMC. Results are
for various small cluster sizes 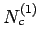 at
at 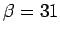 ,
,
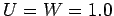 , and
, and 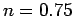 .
.
- 3.12. Spin and charge velocities (
 and
and 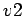 respectively)
obtained by fitting the different results with the
Luttinger Green's functions (Eq. 3.26) about cluster
momentum
respectively)
obtained by fitting the different results with the
Luttinger Green's functions (Eq. 3.26) about cluster
momentum 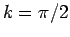 for
for 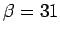 ,
, 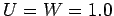 , and
, and 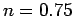 .
Multi-scale results are for a small cluster size
.
Multi-scale results are for a small cluster size
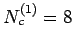 and
different large cluster sizes, and the QMC velocities were obtained
from a single 32 site cluster calculation.
and
different large cluster sizes, and the QMC velocities were obtained
from a single 32 site cluster calculation.
- 3.13. Imaginary part of the self-energy at lowest Matsubara
frequency as obtained by the MSMB method using second order
approximated and full QMC evaluated
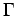 s in comparison to a
large single cluster QMC results at
s in comparison to a
large single cluster QMC results at 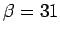 ,
,
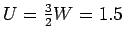 , and
, and
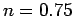 . Multi-scale results are for cluster sizes
. Multi-scale results are for cluster sizes
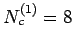 and
and
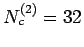 .
.
- 3.14. Imaginary part of the self-energy at lowest Matsubara
frequency as obtained by the MSMB method using the second order
approximated
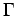 in conjunction with the real-space and
momentum-space based Ansatz at
in conjunction with the real-space and
momentum-space based Ansatz at 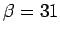 ,
, 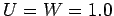 , and
, and
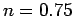 . Also shown is the large single-cluster QMC result.
Multi-scale results are for cluster sizes
. Also shown is the large single-cluster QMC result.
Multi-scale results are for cluster sizes
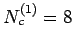 and
and
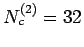 .
.
- 3.15. Parquet equation relating the transverse particle-hole irreducible vertex
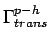 to the fully irreducible vertex
to the fully irreducible vertex 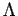 plus contributions from the
longitudinal and particle-particle cross channels. Similar relations
apply for the remaining channels (not shown).
plus contributions from the
longitudinal and particle-particle cross channels. Similar relations
apply for the remaining channels (not shown).
- 3.16. Lowest order non-local corrections to the fully-irreducible
vertex
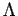 (left) and the vertex
(left) and the vertex 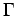 (right).
(right).
- 4.1. Schematic representation of the Dyson equation (upper).
In the SCBA approximation the self-energy is a summation of all non-crossing diagrams (middle)
and can be determined self-consistently using Eq. 4.20 (bottom).
- 4.2. Numerically exact QMC (diamonds) and SCBA (squares) results for polaron
energy
 (a)
and quasiparticle weight
(a)
and quasiparticle weight 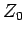 (b) versus the dimensionless electron-phonon coupling
(b) versus the dimensionless electron-phonon coupling 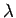 (see Eq. 4.7) at
(see Eq. 4.7) at 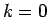 . Holstein model with
. Holstein model with 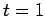 and
and
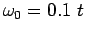 and
and 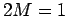 .
.
- 4.3. Holstein polaron dispersion
 (a) and quasiparticle weight
(a) and quasiparticle weight 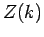 (b)
calculated with SCBA (dotted line) and QMC (circles).
c) Spectral representation obtained with SCBA.
Everywhere
(b)
calculated with SCBA (dotted line) and QMC (circles).
c) Spectral representation obtained with SCBA.
Everywhere
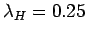 and
and
 .
.
- 4.4. H (circles) and B (diamonds) polaron energy (a) and
quasiparticle weight (b) versus
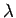 at
at 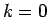 and
and
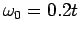 . The open symbols are
the results obtained after only one iteration (first order in
. The open symbols are
the results obtained after only one iteration (first order in 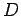 ). The dashed line in (b) corresponds to
). The dashed line in (b) corresponds to
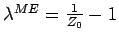 (see Eq. 4.16).
(see Eq. 4.16).
- 4.5. The quasiparticle
weight
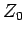 (a) and the polaron energy
(a) and the polaron energy  (b) at zero momentum versus phonon frequency
(b) at zero momentum versus phonon frequency
 for the H and B models at
for the H and B models at
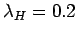 and respectively
and respectively
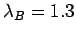 .
.
- 4.6. Quasiparticle weight
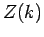 (a) and the polaron energy
(a) and the polaron energy  (b) for the
H and B model for
(b) for the
H and B model for
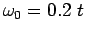 at coupling
at coupling
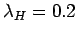 and
and
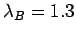 respectively. The dotted horizontal lines in (b) marks the first phonon
threshold energy
respectively. The dotted horizontal lines in (b) marks the first phonon
threshold energy
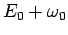 .
.
- 4.7. Spectral representation for:
a) H model,
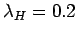 , tight binding dispersion,
b) B model,
, tight binding dispersion,
b) B model,
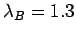 , tight binding dispersion,
c) B model,
, tight binding dispersion,
c) B model,
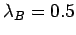 , tight binding dispersion,
d) B model,
, tight binding dispersion,
d) B model,
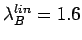 , linear dispersion with
, linear dispersion with 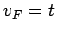 (Eq. 4.25),
e) H model,
(Eq. 4.25),
e) H model,
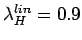 , linear dispersion with
, linear dispersion with 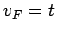 ,
f) H and B model,
,
f) H and B model,
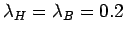 , with dispersion
, with dispersion
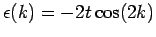 .
Everywhere
.
Everywhere
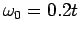 .
The arrows indicate the first (lower) and the second
(upper) phonon threshold energies corresponding to
.
The arrows indicate the first (lower) and the second
(upper) phonon threshold energies corresponding to
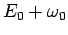 and respectively
and respectively
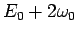 .
.
- 4.8. Spectral function (energy distribution curves) for a) H model with
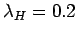 and
b) B model with
and
b) B model with
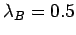 . Free electron tight binding dispersion and
. Free electron tight binding dispersion and
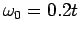 is considered.
is considered.
- 4.9. Spectral function (energy distribution curves) for a) H model with
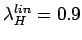 and
b) B model with
and
b) B model with
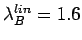 . Free electron linear dispersion
(
. Free electron linear dispersion
(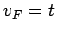 ) and
) and
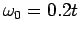 is considered.
is considered.
- 4.10. a) Energy levels for zero coupling (
 ). The solid line shows the non-interacting
electron dispersion, the dashed ones are one phonon + one electron states and the dotted one
two phonons + one electron, etc.
). The solid line shows the non-interacting
electron dispersion, the dashed ones are one phonon + one electron states and the dotted one
two phonons + one electron, etc.  is the momentum where the electron dispersion reaches
is the momentum where the electron dispersion reaches
 and has the most significant contribution to the scattering at the first phonon threshold.
and has the most significant contribution to the scattering at the first phonon threshold. 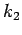 is the value of
momentum with significant contribution to the scattering at the second phonon threshold.
b) For the polaron with momentum
is the value of
momentum with significant contribution to the scattering at the second phonon threshold.
b) For the polaron with momentum 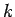 the scattering with momentum
the scattering with momentum 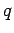 has a significant
contribution.
Although the polaron momentum is close to
has a significant
contribution.
Although the polaron momentum is close to 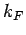 , thus
, thus 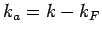 is small,
is small,
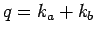 is large because
is large because 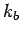 which connects two points on the Fermi
surface can be large.
which connects two points on the Fermi
surface can be large.
© Cyrill Slezak