



Next: 2.2.3 Calculation of physical
Up: 2.2 Mapping to a
Previous: 2.2.1 Principles of the
Now we will compare this system of differential equations with the flow
equations for a resonant level model (RLM). This will lead
to the key result of this chapter: the RLM can
be used as an effective model for the complicated strong-coupling Kondo
model.
The Hamiltonian of the resonant level model is
given by
 |
(2.8) |
Following the same flow equation approach as previously in the SIKM, we
establish a solution to the RLM (2.8). A detailed description of
the flow equation solution
can be found in Ref. (20). One finds the following flow equations
for the parameters in (2.8)
It should be noted that this yields the exact
analytical solution. Having established the flow equations to solve
both the SIKM and the
RLM, respectively, one can now show an approximate equivalence of these two
models. We introduce the substitution
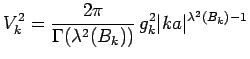 |
|
|
(2.12) |
and notice that with this substitution the two set of flow equations
(2.5,2.6) and (2.9-2.11) become equivalent for
 in the RLM, with the exception of
the logarithmic term in (2.5).
Thus we now have established an approximate mapping of the SIKM onto the RLM
by means of (2.12) in the sense that their flow equation
diagonalization is identical.
We shall refer to this relation by introducing the
effective hybridization function
in the RLM, with the exception of
the logarithmic term in (2.5).
Thus we now have established an approximate mapping of the SIKM onto the RLM
by means of (2.12) in the sense that their flow equation
diagonalization is identical.
We shall refer to this relation by introducing the
effective hybridization function
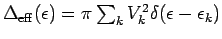 :
the RLM with this non-trivial hybridization function can be used
as an effective model for the SIKM in the Kondo limit (small coupling
limit)
:
the RLM with this non-trivial hybridization function can be used
as an effective model for the SIKM in the Kondo limit (small coupling
limit)
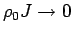 .
Since this noninteracting RLM is a simple, quadratic Hamiltonian, this mapping
will allow us to read off and understand many properties of the complicated
many-body Kondo physics in an intuitive and straightforward way.
It will turn out that the deviations of
.
Since this noninteracting RLM is a simple, quadratic Hamiltonian, this mapping
will allow us to read off and understand many properties of the complicated
many-body Kondo physics in an intuitive and straightforward way.
It will turn out that the deviations of
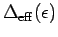 from
a constant hybridization function encode the quasiparticle interaction
and therefore the many-body Kondo physics in this quadratic effective
Hamiltonian.
from
a constant hybridization function encode the quasiparticle interaction
and therefore the many-body Kondo physics in this quadratic effective
Hamiltonian.
Notice that the above mapping between the SIKM and the RLM becomes exact
at the Toulouse point (21)
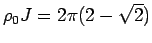 since
since
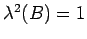 for all flow parameters
for all flow parameters 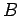 . One easily verifies that the effective RLM
then has a constant hybridization function,
. One easily verifies that the effective RLM
then has a constant hybridization function,
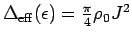 .
In this case, our mapping just reduces to the observation already made
by Toulouse that the partition function of the Kondo model for
this specific coupling constant
.
In this case, our mapping just reduces to the observation already made
by Toulouse that the partition function of the Kondo model for
this specific coupling constant 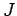 is exactly
equivalent to the partition function of a quadratic Hamiltonian.(21)
is exactly
equivalent to the partition function of a quadratic Hamiltonian.(21)
In order to specify the function
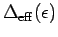 in the Kondo limit
it is best to not directly use relation (2.12), but to determine
the effective hybridization function from matching a correlation
function in the SIKM and the RLM. We have chosen the
in the Kondo limit
it is best to not directly use relation (2.12), but to determine
the effective hybridization function from matching a correlation
function in the SIKM and the RLM. We have chosen the
 -correlation
function, evaluated it with respect to (2.4) for
-correlation
function, evaluated it with respect to (2.4) for  , and
then chose
, and
then chose
 in the RLM such that this
coincided with the
in the RLM such that this
coincided with the
 -correlation function.
The resulting
-correlation function.
The resulting
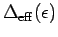 agrees with (2.12)
in the high- and low-energy regimes, with deviations only in the
crossover region. However, the mapping from the Kondo model to the
effective RLM becomes better since this procedure manages to
partly also take the logarithmic term in (2.5) into account.
agrees with (2.12)
in the high- and low-energy regimes, with deviations only in the
crossover region. However, the mapping from the Kondo model to the
effective RLM becomes better since this procedure manages to
partly also take the logarithmic term in (2.5) into account.
The resulting effective hybridization function can
be scaled into a dimensionless form with one dimensionful parameter
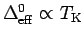
 |
(2.13) |
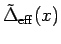 is a universal function in the
Kondo limit (
is a universal function in the
Kondo limit (
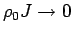 ).
It is depicted in Fig. 2.1 for
).
It is depicted in Fig. 2.1 for
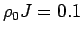 ,
and coincides with its universal form for
,
and coincides with its universal form for
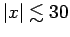 (
(
 , i.e. this should be sufficient
for most practical purposes(22)). For larger energies
the effective hybridization function begins to cross over
into linear behavior with logarithmic corrections
depending on the bare coupling
, i.e. this should be sufficient
for most practical purposes(22)). For larger energies
the effective hybridization function begins to cross over
into linear behavior with logarithmic corrections
depending on the bare coupling 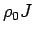 .
.
Figure:
The dimensionless effective hybridization function
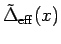 evaluated for
evaluated for
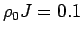 in the SIKM. The resulting function is symmetric and is only plotted for
in the SIKM. The resulting function is symmetric and is only plotted for
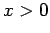 . It coincides with the universal form for
. It coincides with the universal form for
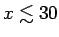 .
The dashed line represents the fit
(2.14) and is nearly indistinguishable from the actual data.
Notice especially the appearance of logarithmic behavior in the
crossover region.
.
The dashed line represents the fit
(2.14) and is nearly indistinguishable from the actual data.
Notice especially the appearance of logarithmic behavior in the
crossover region.
|
|
The following function provides an excellent fit
(see Fig. 2.1)
![$\displaystyle \tilde\Delta_{\rm eff}(x)= \begin{array}[t]{l} \displaystyle 1+ \...
...ht\vert\right)\left( 1-\ln\left\vert\frac{x}{a_0}\right\vert\right) \end{array}$](img158.png) |
(2.14) |
with the parameters from Table 2.1.
Table:
Result of the fit (2.14) to the effective hybridization
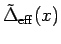 .
.
|
|
A similar analysis based on the comparison of flow equations shows that
the above mapping between the SIKM and the noninteracting RLM can be
extended to the case of a Kondo Hamiltonian (2.1) with a
nonvanishing local magnetic field 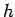
 |
(2.15) |
by setting
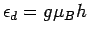 in the RLM.
However, the mapping with the above effective hybridization function becomes
less accurate for
in the RLM.
However, the mapping with the above effective hybridization function becomes
less accurate for
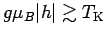 due to the approximate nature of the
flow equation solution (2.5-2.7). We will discuss this
point in more detail below.
due to the approximate nature of the
flow equation solution (2.5-2.7). We will discuss this
point in more detail below.
Summing up, as long as we are interested in static quantities in
a local magnetic field smaller than approximately 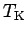 and/or dynamical
correlation functions for energies smaller than approximately
and/or dynamical
correlation functions for energies smaller than approximately
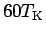 ,
we can use the RLM with the effective hybridization function (2.14)
to describe the physics of the SIKM in the small coupling limit.
The only undetermined parameter in the RLM is the energy scale
,
we can use the RLM with the effective hybridization function (2.14)
to describe the physics of the SIKM in the small coupling limit.
The only undetermined parameter in the RLM is the energy scale
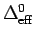 that explicitly depends on
that explicitly depends on 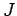 . This overall
energy scale is proportional to
. This overall
energy scale is proportional to 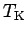 . Notice that the
non-perturbative behavior of this energy scale
. Notice that the
non-perturbative behavior of this energy scale
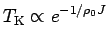 |
(2.16) |
follows correctly from the original flow equations (2.5-2.7),
compare Ref. (16).




Next: 2.2.3 Calculation of physical
Up: 2.2 Mapping to a
Previous: 2.2.1 Principles of the
© Cyrill Slezak

![]() since
since
![]() for all flow parameters
for all flow parameters ![]() . One easily verifies that the effective RLM
then has a constant hybridization function,
. One easily verifies that the effective RLM
then has a constant hybridization function,
![]() .
In this case, our mapping just reduces to the observation already made
by Toulouse that the partition function of the Kondo model for
this specific coupling constant
.
In this case, our mapping just reduces to the observation already made
by Toulouse that the partition function of the Kondo model for
this specific coupling constant ![]() is exactly
equivalent to the partition function of a quadratic Hamiltonian.(21)
is exactly
equivalent to the partition function of a quadratic Hamiltonian.(21)
![]() in the Kondo limit
it is best to not directly use relation (2.12), but to determine
the effective hybridization function from matching a correlation
function in the SIKM and the RLM. We have chosen the
in the Kondo limit
it is best to not directly use relation (2.12), but to determine
the effective hybridization function from matching a correlation
function in the SIKM and the RLM. We have chosen the
![]() -correlation
function, evaluated it with respect to (2.4) for
-correlation
function, evaluated it with respect to (2.4) for ![]() , and
then chose
, and
then chose
![]() in the RLM such that this
coincided with the
in the RLM such that this
coincided with the
![]() -correlation function.
The resulting
-correlation function.
The resulting
![]() agrees with (2.12)
in the high- and low-energy regimes, with deviations only in the
crossover region. However, the mapping from the Kondo model to the
effective RLM becomes better since this procedure manages to
partly also take the logarithmic term in (2.5) into account.
agrees with (2.12)
in the high- and low-energy regimes, with deviations only in the
crossover region. However, the mapping from the Kondo model to the
effective RLM becomes better since this procedure manages to
partly also take the logarithmic term in (2.5) into account.
![]()
![\includegraphics[width=0.9\textwidth,clip]{hyb_appr}](img157.png)
![]()
![]() and/or dynamical
correlation functions for energies smaller than approximately
and/or dynamical
correlation functions for energies smaller than approximately
![]() ,
we can use the RLM with the effective hybridization function (2.14)
to describe the physics of the SIKM in the small coupling limit.
The only undetermined parameter in the RLM is the energy scale
,
we can use the RLM with the effective hybridization function (2.14)
to describe the physics of the SIKM in the small coupling limit.
The only undetermined parameter in the RLM is the energy scale
![]() that explicitly depends on
that explicitly depends on ![]() . This overall
energy scale is proportional to
. This overall
energy scale is proportional to ![]() . Notice that the
non-perturbative behavior of this energy scale
. Notice that the
non-perturbative behavior of this energy scale