



Next: 2.3 Results
Up: 2.2 Mapping to a
Previous: 2.2.2 Equivalence to a
Once the mapping between the SIKM (2.1) and the effective
RLM (2.8)
has been established, one can readily calculate
physical quantities for the Kondo model. One complication arises from the fact
that operators of the
original SIKM have to be transformed by a unitary transformation analogous to
(2.2). In the
language of the effective resonant level model they will thus in general
correspond to more complicated
many-particle operators. Since the intention of this chapter is to demonstrate the
potential of our mapping in a pedagogical setting, we will
concentrate on two quantities that remain simple under these
transformations:
i) the 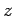 -component of the spin operator
-component of the spin operator  , which becomes
, which becomes
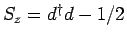 , and ii) the Hamiltonian itself.
, and ii) the Hamiltonian itself.
From the latter we obtain the
internal energy
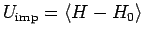 and the Sommerfeld coefficient,
and the Sommerfeld coefficient,
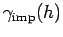 .
A straightforward calculation in the noninteracting RLM yields
.
A straightforward calculation in the noninteracting RLM yields
 |
(2.17) |
where
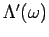 denotes the derivative of
and
denotes the derivative of
and
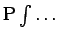 is the principal value integral.
Here
is the principal value integral.
Here
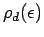 is the impurity orbital density of states
of the RLM
is the impurity orbital density of states
of the RLM
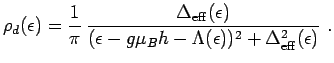 |
(2.18) |
The result (2.17) for
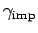 has some interesting
implications. First, because
has some interesting
implications. First, because
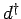 is connected to
is connected to 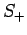 , it is apparent that the low-energy excitations
in the system
are controlled by spin degrees of freedom, a well-known feature of the Kondo
physics. However,
in our approach this result can be read off directly from
equ. (2.17). Second,
, it is apparent that the low-energy excitations
in the system
are controlled by spin degrees of freedom, a well-known feature of the Kondo
physics. However,
in our approach this result can be read off directly from
equ. (2.17). Second,
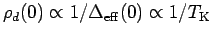 , i.e. we obtain the
correct scaling behavior
for
, i.e. we obtain the
correct scaling behavior
for
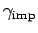 directly from the behavior of
directly from the behavior of
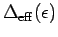 . There is, however,
a nontrivial correction coming from the factor in parenthesis in
(2.17). Note that for
. There is, however,
a nontrivial correction coming from the factor in parenthesis in
(2.17). Note that for
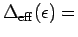 const. this
correction is one, but for the strongly
const. this
correction is one, but for the strongly 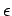 -dependent
-dependent
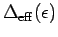 in Fig. 2.1 it is of the order of two. As we
will demonstrate later,
this difference is directly responsible for obtaining the correct Wilson ratio
in our approach.
in Fig. 2.1 it is of the order of two. As we
will demonstrate later,
this difference is directly responsible for obtaining the correct Wilson ratio
in our approach.
From the mapping
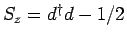 it is easy to calculate
it is easy to calculate
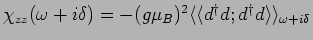 . Since
the correlation
function has to be evaluated within the RLM, one obtains for
the imaginary part
at
. Since
the correlation
function has to be evaluated within the RLM, one obtains for
the imaginary part
at 
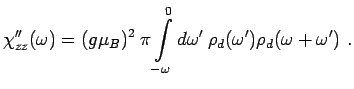 |
(2.19) |
Again, this result provides direct access to an interpretation of the behavior
of
 in terms of the physics of the resonant level model.
in terms of the physics of the resonant level model.




Next: 2.3 Results
Up: 2.2 Mapping to a
Previous: 2.2.2 Equivalence to a
© Cyrill Slezak
![]() and the Sommerfeld coefficient,
and the Sommerfeld coefficient,
![]() .
A straightforward calculation in the noninteracting RLM yields
.
A straightforward calculation in the noninteracting RLM yields
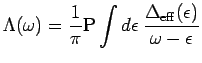
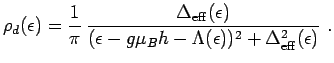
![]() has some interesting
implications. First, because
has some interesting
implications. First, because
![]() is connected to
is connected to ![]() , it is apparent that the low-energy excitations
in the system
are controlled by spin degrees of freedom, a well-known feature of the Kondo
physics. However,
in our approach this result can be read off directly from
equ. (2.17). Second,
, it is apparent that the low-energy excitations
in the system
are controlled by spin degrees of freedom, a well-known feature of the Kondo
physics. However,
in our approach this result can be read off directly from
equ. (2.17). Second,
![]() , i.e. we obtain the
correct scaling behavior
for
, i.e. we obtain the
correct scaling behavior
for
![]() directly from the behavior of
directly from the behavior of
![]() . There is, however,
a nontrivial correction coming from the factor in parenthesis in
(2.17). Note that for
. There is, however,
a nontrivial correction coming from the factor in parenthesis in
(2.17). Note that for
![]() const. this
correction is one, but for the strongly
const. this
correction is one, but for the strongly ![]() -dependent
-dependent
![]() in Fig. 2.1 it is of the order of two. As we
will demonstrate later,
this difference is directly responsible for obtaining the correct Wilson ratio
in our approach.
in Fig. 2.1 it is of the order of two. As we
will demonstrate later,
this difference is directly responsible for obtaining the correct Wilson ratio
in our approach.
![]() it is easy to calculate
it is easy to calculate
![]() . Since
the correlation
function has to be evaluated within the RLM, one obtains for
the imaginary part
at
. Since
the correlation
function has to be evaluated within the RLM, one obtains for
the imaginary part
at ![]()