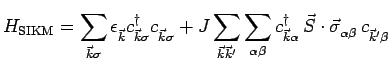2.1 Introduction

The single impurity Kondo or $s$-$d$ model (SIKM) (1)

$$H_{\rm SIKM} = \sum\limits_{\vec k\sigma}\epsilon^{\phantom{\dagg... ...\sigma^{\phantom{\dagger}}_{\alpha\beta}\, c^{\phantom{\dagger}}_{\vec k'\beta}$$ (2.1)

is, together with its close relative, the single impurity Anderson model (SIAM) (2), one of the fundamental models in the theory of correlated electron systems. It has been studied extensively over the past four decades (3), but despite its simplicity, no complete analytic solution exists that provides information on both thermodynamic and dynamical quantities. For example, the Bethe ansatz solution (3,4) has solved all universal properties of the Kondo problem including its high- to low-temperature crossover behavior. But the Bethe ansatz requires the limit of infinite conduction band width and cannot be used to calculate dynamical quantities beyond the low-energy limit.

Thus, numerical methods, like Wilson's numerical renormalization group (NRG) (3,5) or quantum Monte-Carlo (QMC) (6), in connection with maximum-entropy methods (7) have to be employed to access dynamical quantities on all energy scales. In both methods, evaluation of dynamical properties, and quantities related to them, like the Korringa-Shiba relation or the Friedel sum rule (3), suffer from unavoidable numerical errors. QMC simulations, in addition, cannot be used at zero temperature and are restricted to comparatively large values of $J$.(6) Moreover, a reliable evaluation of single- and two-particle spectra and related quantities in an external magnetic field, as well as their comparison and interpretation within a local Fermi liquid picture (3) become rather problematic (8,9), especially in the limit of vanishing external magnetic field. Approximate analytical techniques, like perturbation expansions or $1/N$-expansions (3), typically only describe certain properties of the Kondo model correctly. A notable exception in this respect is the so-called local moment approach (LMA) (10). This perturbative approach is very accurate in most cases (11), including those of nonvanishing external magnetic fields.(12,9)

Besides its relevance for the study of moment formation in metals, the SIKM (2.1) has gained new importance as input for investigating non-dilute correlated electron systems like heavy fermion materials within dynamical mean-field theory (DMFT).(13) Here a reliable method for calculating single-particle correlation functions, especially close to the Fermi energy, is extremely important.

In this chapter, we propose a new non-perturbative semi-analytical approach to the Kondo problem based on Wegner's flow equation method (14) and previous work on applications of flow equations to strong-coupling problems (15,16). We will show that to a very good approximation, many physical quantities of the Kondo model can be calculated from a resonant level model (RLM), where the interacting features of the Kondo model are encoded in a non-constant effective hybridization function of this resonant level model. Surprisingly, this noninteracting effective model describes both universal low-energy properties like the Wilson ratio as well as high-energy power laws and logarithmic corrections with very good accuracy. Due to the noninteracting nature of this effective model this mapping allows immediate insights into the physics of the SIKM, for example the dependence of its static and dynamical quantities on a local magnetic field.

After presenting our approach in the next section, we will discuss several static quantities at $T=0$ as a function of a local magnetic field and derive analytical expressions for their asymptotic behavior. As an example for a dynamical quantity, we will then discuss the spin-structure factor and the Korringa-Shiba relation. An outlook on potential future applications of our approach concludes this chapter.