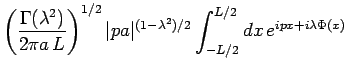Next: 2.2.2 Equivalence to a
Up: 2.2 Mapping to a
Previous: 2.2 Mapping to a
The general framework of the flow equation method(14) and its
application to the Kondo model has been explained in detail in
Ref. (16).
Here we will only repeat the main steps in order to make this chapter self-contained,
and refer to Ref. (16) for more details.
The key idea of the flow equation approach consists in performing a continuous
sequence of infinitesimal unitary transformations on a given Hamiltonian
![$\displaystyle \frac{dH(B)}{dB}=[\eta(B),H(B)] \ .$](img94.png) |
(2.2) |
With an anti-Hermitian generator 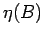 the solution of equation
(2.2) describes a family of unitarily equivalent Hamiltonians
the solution of equation
(2.2) describes a family of unitarily equivalent Hamiltonians
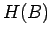 parameterized by the flow parameter
parameterized by the flow parameter 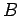 . By choosing
. By choosing
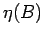 appropriately(14) one can set up a framework that
diagonalizes a many-particle Hamiltonian
appropriately(14) one can set up a framework that
diagonalizes a many-particle Hamiltonian 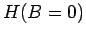 , i.e.
, i.e.
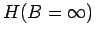 becomes diagonal.
becomes diagonal.
The concrete realization of this
approach for the Kondo model was discussed in Ref. (16).
The starting point is the bosonized form(17) of the
Hamiltonian (2.1).
Since we will be mainly interested in describing the basic ideas of our
approach, we restrict ourselves to a linear dispersion relation.
Notice, however, that the flow equation approach can also be used
for a nontrivial conduction band density of states as it does not rely
on the integrability of the model.(18)
With a linear dispersion relation
the Kondo problem becomes effectively one-dimensional,
the charge density excitations in (2.1) decouple, and we only need
to look at the spin density part
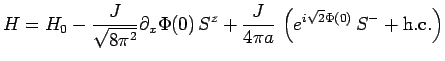 |
(2.3) |
with
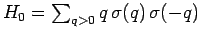 .
Here
.
Here
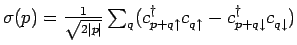 are the bosonic spin density modes with the bosonic spin density field defined by
are the bosonic spin density modes with the bosonic spin density field defined by
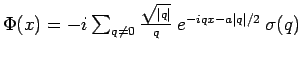 . For simplicity we have set the
Fermi velocity
. For simplicity we have set the
Fermi velocity 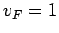 .
.  is proportional to the inverse conduction
band width. All our latter results will be expressed as universal
functions of the low-energy Kondo scale
is proportional to the inverse conduction
band width. All our latter results will be expressed as universal
functions of the low-energy Kondo scale 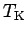 , and we can consider
(2.3) to be equivalent to our original Kondo Hamiltonian
if
, and we can consider
(2.3) to be equivalent to our original Kondo Hamiltonian
if
 .
.
Eq. (2.3) was used as the starting point 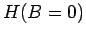 of the flow equation approach in Ref. (16). Away
from the Toulouse point the unitary equivalence of the flow holds only
approximately, but this approximation can be controlled by a small
parameter(15) and yields very accurate
results. During the flow the Hamiltonian can be parameterized as
of the flow equation approach in Ref. (16). Away
from the Toulouse point the unitary equivalence of the flow holds only
approximately, but this approximation can be controlled by a small
parameter(15) and yields very accurate
results. During the flow the Hamiltonian can be parameterized as
Here
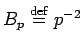 , and
, and
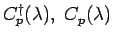 denote normalized vertex operators
with scaling dimension
denote normalized vertex operators
with scaling dimension 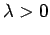 in momentum space,
in momentum space,
that obey
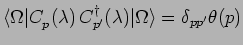 and
and
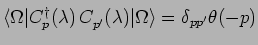 .
For the special case
.
For the special case 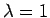 they fulfill fermionic anticommutation relations
they fulfill fermionic anticommutation relations
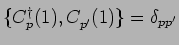 and can therefore be interpreted
as creation and annihilation operators for fermions.
and can therefore be interpreted
as creation and annihilation operators for fermions.
In Ref. (16) the following flow equations for the
parameters in (2.4) have been derived
and a differential equation for the flow of the scaling dimension
 |
(2.7) |
It can be shown(16) that
one always finds
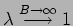 in the strong-coupling phase of the Kondo model,
i.e. in the low-energy limit the vertex operators in (2.4)
become fermions. In the following we will use an improved version of
the above flow equations by taking into account that all approximations
should be performed with respect to the interacting ground state:
It turns out that the only necessary modification in (2.5), (2.6)
and (2.7) is that the exponent in
in the strong-coupling phase of the Kondo model,
i.e. in the low-energy limit the vertex operators in (2.4)
become fermions. In the following we will use an improved version of
the above flow equations by taking into account that all approximations
should be performed with respect to the interacting ground state:
It turns out that the only necessary modification in (2.5), (2.6)
and (2.7) is that the exponent in
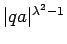 gets replaced by
gets replaced by
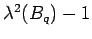 , i.e. it is not a running exponent
anymore.(19)
, i.e. it is not a running exponent
anymore.(19)




Next: 2.2.2 Equivalence to a
Up: 2.2 Mapping to a
Previous: 2.2 Mapping to a
© Cyrill Slezak
![$\displaystyle \frac{dH(B)}{dB}=[\eta(B),H(B)] \ .$](img94.png)
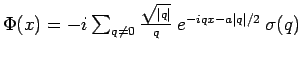 . For simplicity we have set the
Fermi velocity
. For simplicity we have set the
Fermi velocity ![]() of the flow equation approach in Ref. (16). Away
from the Toulouse point the unitary equivalence of the flow holds only
approximately, but this approximation can be controlled by a small
parameter(15) and yields very accurate
results. During the flow the Hamiltonian can be parameterized as
of the flow equation approach in Ref. (16). Away
from the Toulouse point the unitary equivalence of the flow holds only
approximately, but this approximation can be controlled by a small
parameter(15) and yields very accurate
results. During the flow the Hamiltonian can be parameterized as
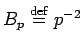 , and
, and