



Next: 4.2.3 Method
Up: 4.2 Formalism
Previous: 4.2.1 Model
4.2.2 Electron-Phonon Coupling
In this chapter, we define the dimensionless
electron-phonon coupling as
the ratio of the lattice deformation energy of a localized electron
and the kinetic (delocalization) energy of the electron.
This definition is encountered mostly in polaron studies focusing on the transition
from large to small polarons (30,28).
For the Holstein model the deformation energy is given by (see Eq. 4.37)
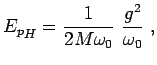 |
(4.6) |
and the dimensionless coupling is defined as
 |
(4.7) |
where the half-bandwidth 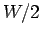 is taken as a measure of the free electron
kinetic energy. For a simple tight binding dispersion
is taken as a measure of the free electron
kinetic energy. For a simple tight binding dispersion 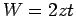 , where
, where
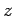 is the coordination number.
is the coordination number.
Analogously, for the breathing model the lattice deformation energy is (see
Appendix 4.6.2)
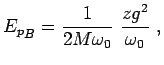 |
(4.8) |
and the dimensionless coupling is hence defined as
 |
(4.9) |
Compared to the Holstein case, the lattice deformation energy for
the breathing model has an extra factor of 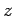 as can be seen in Eq. 4.8,
which results form the fact that the electron interacts with
as can be seen in Eq. 4.8,
which results form the fact that the electron interacts with 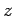 neighboring oscillators.
neighboring oscillators.
There are several other definitions for the dimensionless electron-phonon coupling
throughout the literature. For instance in the BCS theory the definition of the dimensionless coupling
is
 , where
, where 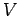 and
and  are the effective electron-electron attraction
and respectively the density of states at the Fermi level.
In the weak coupling regime the effective interaction at
small frequency or in the antiadiabatic limit (
are the effective electron-electron attraction
and respectively the density of states at the Fermi level.
In the weak coupling regime the effective interaction at
small frequency or in the antiadiabatic limit (
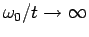 ) is
) is
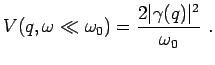 |
(4.10) |
If the integration over all 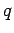 momenta is considered for the breathing model, then
momenta is considered for the breathing model, then
When choosing the density of states  ,
this definition of the dimensionless coupling coincides with our definition.
,
this definition of the dimensionless coupling coincides with our definition.
In the Migdal-Eliashberg theory of superconductivity,
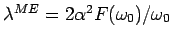 where only scattering processes at the Fermi surface are
considered (31,32) in
where only scattering processes at the Fermi surface are
considered (31,32) in
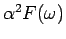 . This definition is equivalent
to(32)
. This definition is equivalent
to(32)
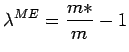 |
(4.13) |
where 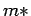 is the quasiparticle renormalized effective mass at the Fermi surface.
is the quasiparticle renormalized effective mass at the Fermi surface.
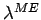 can be directly determined from experiments
since
can be directly determined from experiments
since
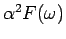 and
and 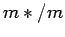 can be measured in tunneling (33),
neutron (34) or respectively in the ARPES experiments (2).
In our case, the effective mass at the bottom of the band (which is the
zero energy state of our system and in many respects similar to the Fermi surface in a many-electron system)
can be determined from the equation
can be measured in tunneling (33),
neutron (34) or respectively in the ARPES experiments (2).
In our case, the effective mass at the bottom of the band (which is the
zero energy state of our system and in many respects similar to the Fermi surface in a many-electron system)
can be determined from the equation
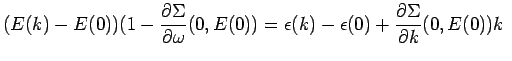 |
(4.14) |
valid at small 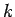 . The ratio of the effective mass and the un-renormalized mass is
. The ratio of the effective mass and the un-renormalized mass is
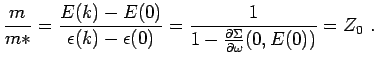 |
(4.15) |
Therefore, we have
 |
(4.16) |
This definition directly relates the quasiparticle weight 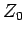 to the coupling constant
to the coupling constant
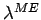 .
In the first order perturbation theory one gets
.
In the first order perturbation theory one gets
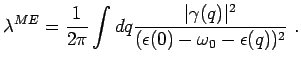 |
(4.17) |
By inspecting Eq. 4.17 one can see that the most important contribution
to the integral comes form small 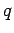 where the denominator is small. For the B model this will
introduce a significant difference between
where the denominator is small. For the B model this will
introduce a significant difference between
 and our
and our 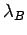 (Eq. 4.9). Unlike our definition which assumes average over all possible phonon
momenta,
(Eq. 4.9). Unlike our definition which assumes average over all possible phonon
momenta,
 is determined by small
is determined by small 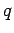 phonon scatterings which are characterized
by small
phonon scatterings which are characterized
by small 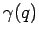 in the B model.
in the B model.
The definition of
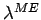 used in the Migdal-Eliashberg theory
was intended to describe the properties at the Fermi level or at small energy excitation.
It does not properly describe the physics at larger energy since the most
relevant scattering processes in this case imply larger phonon momenta as we will
discuss in the next two sections.
used in the Migdal-Eliashberg theory
was intended to describe the properties at the Fermi level or at small energy excitation.
It does not properly describe the physics at larger energy since the most
relevant scattering processes in this case imply larger phonon momenta as we will
discuss in the next two sections.




Next: 4.2.3 Method
Up: 4.2 Formalism
Previous: 4.2.1 Model
© Cyrill Slezak
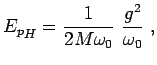
![]() , where
, where ![]() and
and ![]() are the effective electron-electron attraction
and respectively the density of states at the Fermi level.
In the weak coupling regime the effective interaction at
small frequency or in the antiadiabatic limit (
are the effective electron-electron attraction
and respectively the density of states at the Fermi level.
In the weak coupling regime the effective interaction at
small frequency or in the antiadiabatic limit (
![]() ) is
) is
![]() where only scattering processes at the Fermi surface are
considered (31,32) in
where only scattering processes at the Fermi surface are
considered (31,32) in
![]() . This definition is equivalent
to(32)
. This definition is equivalent
to(32)
![]() used in the Migdal-Eliashberg theory
was intended to describe the properties at the Fermi level or at small energy excitation.
It does not properly describe the physics at larger energy since the most
relevant scattering processes in this case imply larger phonon momenta as we will
discuss in the next two sections.
used in the Migdal-Eliashberg theory
was intended to describe the properties at the Fermi level or at small energy excitation.
It does not properly describe the physics at larger energy since the most
relevant scattering processes in this case imply larger phonon momenta as we will
discuss in the next two sections.