4.6.1 Holstein

The last two terms of the Holstein Hamiltonian (Eq. 4.1) can be diagonalized via the Lang-Firsov canonical transformation(39) defined by a unitary operator $e^S$ where

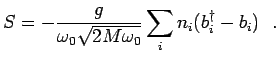$$S=-\frac{g}{\omega_0 \sqrt{2 M \omega_0}}\sum_{i} n_i(b^{\dagger}_i -b_i)~~.$$ (4.28)

Using the expansion

$$\tilde{A}=e^SAe^{-S}=A+[S,A]+\frac{1}{2}[S,[S,A]]+...$$ (4.29)

we find for the transformed phonon annihilation operator:

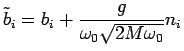$$\tilde{b}_i=b_i+\frac {g}{\omega_0\sqrt{2 M \omega_0}}n_i$$ (4.30)

and similarly for the electron operator

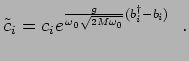$$\tilde{c}_i=c_i e^{\frac{g}{\omega_0 \sqrt{2 M \omega_0}}(b^\dagger_i-b_i)}~~.$$ (4.31)

The tilde mark is used to label the transformed operators. The Holstein Hamiltonian in the new basis can be written as

$$H=H_0+H_t$$ (4.32)

$$H_0=\sum_{i}\omega_0 \tilde{b}^\dagger_i \tilde{b}_i - \frac{g^2}{2 M\omega_0^2}\sum_{i}\tilde{n}_i^2$$ (4.33)

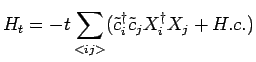$$H_t=-t\sum_{<ij>}(\tilde{c}^\dagger_i \tilde{c}_j X^\dagger _i X_j+H.c.)$$ (4.34)

where

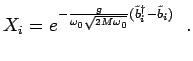$$X_i=e^{-\frac{g}{\omega_0\sqrt{2 M \omega_0}}(\tilde{b}^\dagger_i-\tilde{b}_i)}~~.$$ (4.35)

For a single electron the density term in Eq. 4.33 simplifies, yielding

$$H_0=\sum_{i}\omega_0 \tilde{b}^\dagger_i \tilde{b}_i - \frac{g^2}{2 M \omega_0^2}\sum_{i}\tilde{n}_i$$ (4.36)

One can define a dimensionless coupling constant for the electron-phonon interaction as the ratio between the gained lattice deformation energy (see second term in $H_0$)

$${E_p}_H= \frac{1}{2M\omega_0}~ \frac{g^2}{\omega_0}~,$$ (4.37)

and the bare electron kinetic energy, taken to be the half-bandwidth, $W/2=zt$,

$$\lambda_H= \frac{2{E_p}_H}{W}=\frac{1}{2M\omega_0}\frac{g^2}{z\omega_0t}~.$$ (4.38)