4.6.2 Breathing

The electron-phonon interaction term in the B Hamiltonian (see last term in Eq. 4.2) can, by changing the order of summation, be re-write it in the form

$$H_{int}=g \sum_{i} x_{i-\frac{1}{2}}(n_i-n_{i-1})~,$$ (4.39)

where $x_i$ is the lattice displacement. The last two parts of the Hamiltonian are once again diagonalized via the unitary operator $e^S$ where

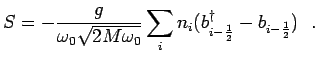$$S=-\frac{g}{\omega_0 \sqrt{2 M \omega_0}}\sum_{i} n_i(b^{\dagger}_{i-\frac{1}{2}} -b_{i-\frac{1}{2}})~~.$$ (4.40)

Using the expansion of Eq. 4.29 we find for the transformed phonon and electron annihilation operators:

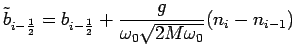$$\tilde{b}_{i-\frac{1}{2}}=b_{i-\frac{1}{2}}+\frac {g}{\omega_0\sqrt{2 M \omega_0}} (n_i-n_{i-1})$$ (4.41)

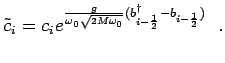$$\tilde{c}_i=c_i e^{\frac{g}{\omega_0 \sqrt{2 M \omega_0}}(b^\dagger_{i-\frac{1}{2}}-b_{i-\frac{1}{2}})}~~.$$ (4.42)

Substituting these transformed operators we find in the new basis

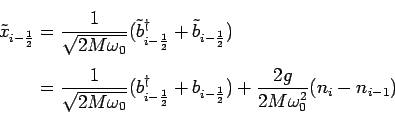$$\begin{split}\tilde{x}_{i-\frac{1}{2}}&=\frac{1}{\sqrt{2M\ome... ...frac{1}{2}}) +\frac{2g}{2 M\omega_0^2}(n_i-n_{i-1}) \end{split}$$ (4.43)

and for the breathing-Hamiltonian

$$H_0=\sum_{i}\omega_0 \tilde{b}^\dagger_i \tilde{b}_i - \frac{g^2}{2 M\omega_0^2}\sum_{i}(\tilde{n}_i-\tilde{n}_{i-1})^2$$ (4.44)

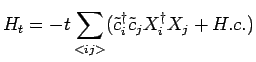$$H_t=-t\sum_{<ij>}(\tilde{c}^\dagger_i \tilde{c}_j X^\dagger _i X_j+H.c.)$$ (4.45)

where

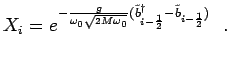$$X_i=e^{-\frac{g}{\omega_0\sqrt{2 M \omega_0}}(\tilde{b}^\dagger_{i-\frac{1}{2}}-\tilde{b}_{i-\frac{1}{2}})}~~.$$ (4.46)

In the case of a system only containing a single electron the density terms contained in Eq. 4.44 simplify, yielding

$$H_0=\sum_{i}\omega_0 \tilde{b}^\dagger_i \tilde{b}_i - \frac{2 g^2}{2 M \omega_0^2}\sum_{i}\tilde{n}_i~~.$$ (4.47)

Hence, the lattice deformation energy is found to be

$${E_p}_B= \frac{1}{2M\omega_0}~ \frac{2 g^2}{\omega_0}~,$$ (4.48)

In contrast to the H model (Eq. 4.37) we incur an additional factor of $2$ due to a coupling with two neighboring oscillators. For higher dimensionality the number of neighboring oscillators is given by the coordination number $z$, thus replacing the factor $2$ in Eq. 4.48 with $z$.

We thus define the dimensionless coupling constant for the electron-breathing-phonon interaction

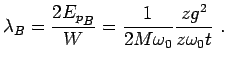$$\lambda_B= \frac{2{E_p}_B}{W}=\frac{1}{2M\omega_0}\frac{zg^2}{z\omega_0t}~.$$ (4.49)

This definition is identical to that found for the Holstein polaron besides the overall factor of $z$.

1.0