To account for the omitted set of short length-scale self-energy
diagrams in the ![]() -approximation, we substitute appropriate
diagrams from the small cluster QMC result. This diagrammatic
substitution between the different length-scales in the MSMB method is
done by means of an analytic Ansatz.
-approximation, we substitute appropriate
diagrams from the small cluster QMC result. This diagrammatic
substitution between the different length-scales in the MSMB method is
done by means of an analytic Ansatz.
One possible implementation of the MSMB method which yields a self-energy containing correlations on both long and short length-scales is given by the real-space Ansatz:
In this formalism, the MSMB self-energy is constructed by taking
all contributions of lengths up to the linear sizes of the small
cluster (
![]() ) from the exact QMC result and the remaining
longer ranged contributions are complemented by the
) from the exact QMC result and the remaining
longer ranged contributions are complemented by the ![]() -approximated
large cluster self-energy. Note, the multi-scale self-energy obtained
in Eq. 3.10 has lost its spatial continuity.
Fourier-transforming the individual length-scale contributions in
Eq. 3.10 yields
-approximated
large cluster self-energy. Note, the multi-scale self-energy obtained
in Eq. 3.10 has lost its spatial continuity.
Fourier-transforming the individual length-scale contributions in
Eq. 3.10 yields
J. Hague et. al. in ref. (3) considered the following, alternative momentum-space Ansatz to combine the different length-scales:
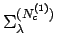 is the self-energy
obtained in the
is the self-energy
obtained in the 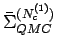 and
and
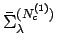 . It is important to note that the coarse
graining in going from large- to small-cluster self-energies is not an
averaging over electron propagators but the term is used in this
context to imply an averaging of the self-energy within a
cluster-cell.
. It is important to note that the coarse
graining in going from large- to small-cluster self-energies is not an
averaging over electron propagators but the term is used in this
context to imply an averaging of the self-energy within a
cluster-cell.
While the real space implementation of the Ansatz was a straight
forward combination of different length-scale elements, the momentum
implementation interpretation is more involved. The ![]() -method
provides an estimate for the set of self-energy diagrams which convey
the long-ranged correlations of the system. However, since in
reciprocal space there isn't an explicit separation of length-scales,
the remaining short length-scale diagrams which are to be supplied by
the QMC calculation have to be identified. This can be accomplished by
removing the sub-set of
-method
provides an estimate for the set of self-energy diagrams which convey
the long-ranged correlations of the system. However, since in
reciprocal space there isn't an explicit separation of length-scales,
the remaining short length-scale diagrams which are to be supplied by
the QMC calculation have to be identified. This can be accomplished by
removing the sub-set of ![]() -approximated self-energy diagrams on
the small cluster from the complete set of the QMC calculation hence
avoiding a double counting of the corresponding self-energy
contributions.
-approximated self-energy diagrams on
the small cluster from the complete set of the QMC calculation hence
avoiding a double counting of the corresponding self-energy
contributions.
Within the traditional form of the DCA, all self-energies are
inherently causal for each individual cluster. One consequence of
causality is that
![]() . In this Ansatz based implementation of the MSMB method however, causality
is not inherently guaranteed. The combination of self-energy
contributions of various length-scales in the Ansatz is only
assured to yield a causal multi-scale self-energy in the limit of the
cluster sizes approaching one another. Therefore, causality in these
schemes cannot be guaranteed and hence has to be monitored closely
throughout. For a more detailed discussion of this and the entire
momentum-space Ansatz see Ref. (3).
. In this Ansatz based implementation of the MSMB method however, causality
is not inherently guaranteed. The combination of self-energy
contributions of various length-scales in the Ansatz is only
assured to yield a causal multi-scale self-energy in the limit of the
cluster sizes approaching one another. Therefore, causality in these
schemes cannot be guaranteed and hence has to be monitored closely
throughout. For a more detailed discussion of this and the entire
momentum-space Ansatz see Ref. (3).
The remaining self-consistent implementation of the multi scale method
(i.e. two cluster DCA) is similar to that of the traditional, single
cluster DCA. Fig. 3.5 depicts a flow chart of the
implementation of both Ansätze in the scheme of the overall
self-consistency loop. The bottom loop shows the already discussed DCA
self-consistency loop using the QMC as a small cluster solver. For the
large cluster solver (![]() -method) the self-consistency is
similar. In the overall scheme of the Ansatz, the two cluster
problems are combined in a fully self-consistent approach: After each
iteration of the QMC/DCA loop, the corresponding
-method) the self-consistency is
similar. In the overall scheme of the Ansatz, the two cluster
problems are combined in a fully self-consistent approach: After each
iteration of the QMC/DCA loop, the corresponding ![]() /DCA
contribution on the large cluster is evaluated. The Ansatz is
used after each step to calculate new estimates for the self-energies
on both the small and large cluster, thus yielding a fully
self-consistent solution. The corresponding paths are shown in
Fig. 3.5. The converged Ansatz
self-energy will be dominated by the small cluster QMC self-energy
which contributes the strongest, short-ranged correlations. The
remaining weaker long-ranged correlations are incorporated in the
difference of
/DCA
contribution on the large cluster is evaluated. The Ansatz is
used after each step to calculate new estimates for the self-energies
on both the small and large cluster, thus yielding a fully
self-consistent solution. The corresponding paths are shown in
Fig. 3.5. The converged Ansatz
self-energy will be dominated by the small cluster QMC self-energy
which contributes the strongest, short-ranged correlations. The
remaining weaker long-ranged correlations are incorporated in the
difference of ![]() -approximated self-energies between the two
clusters. In moving away from a fully self-consistent approach, the
self-consistency restrictions may be lessened to various degrees. Some
possible implementations will be discussed in further detail in
section 3.4.
-approximated self-energies between the two
clusters. In moving away from a fully self-consistent approach, the
self-consistency restrictions may be lessened to various degrees. Some
possible implementations will be discussed in further detail in
section 3.4.