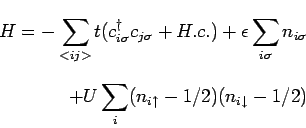 |
(3.1) |
For simplicity, we will use the one dimensional Hubbard model to illustrate the MSMB formalism. This low dimension is also the most difficult regime for quantum cluster approaches like the DCA. The Hubbard Hamiltonian is given by
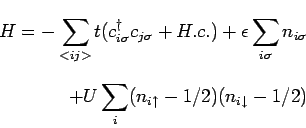 |
(3.1) |
with
![]() creating an electron of spin
creating an electron of spin
![]() at site
at site ![]() and local density
and local density
![]() . The first part, the
kinetic term, allows hopping between adjacent lattice sites with
transfer integral
. The first part, the
kinetic term, allows hopping between adjacent lattice sites with
transfer integral ![]() . The second term is the on-site Coulomb
repulsion making a doubly occupied lattice site unfavorable.
Throughout the remainder of this paper we
choose the bare bandwidth
. The second term is the on-site Coulomb
repulsion making a doubly occupied lattice site unfavorable.
Throughout the remainder of this paper we
choose the bare bandwidth ![]() as the unit of energy by setting
as the unit of energy by setting
![]() and work at fixed filling
and work at fixed filling ![]() .
.