3.4 Technical Aspects

A MSMB approach based on a first order approximated vertex is similar to the limited FLEX-hybrid approach previously considered by J. Hague et. al. (3). In their work the intermediate length-regime was addressed using the FLEX which was incorporated within a multi-scale approach using the fully self-consistent momentum space Ansatz (see Eqs. 3.12 and 3.13). However, in the regime of stronger couplings and/or lower temperatures, where a significant contribution of longer ranged correlations is to be expected, the method fails. In this section we propose changes to the implementation of the multi-scales method which significantly improves its range of applicability by 1) restriction of the Ansatz to the large cluster, 2) modification of the cluster conversion, and 3) removal of the self-consist implementation of the Ansatz on the large cluster.

Figure 3.7: Imaginary part of the self-energy at lowest Matsubara frequency as obtained by various cluster solvers and FLEX/MSMB method at $\beta =8$, $U=W=1.0$, and $n=0.75$. The MSMB cluster sizes are $N_c^{(1)}=8$ and $N_c^{(2)}=32$.

In the original inception(3), the Ansatz is evaluated fully self-consistently within both the QMC and FLEX as discussed in section 3.2.4. The self-energy contributions of these two clusters solvers are linked by the momentum space Ansatz. However, long ranged-correlations, as are described by the large cluster FLEX, are assumed weak. Hence, their presence in the effective medium of the small cluster only minutely effects the QMC self-energy. We thus neglect the Ansatz on the small cluster (Eq. 3.12). With this modification, the small cluster problem can be solved independently of the large cluster problem. This results in a significant reduction in numerical complexity.

With the removal of the small cluster Ansatz condition, only a unidirectionally cluster conversion of small cluster self-energies to the large cluster remains. In this work, a periodic cubic spline interpolation ^3.1 is employed. This provides a good approximation for the multi-scale self-energy in the high temperature/small $U$ limit. Fig. 3.7 shows the imaginary part of the exact, QMC calculated and FLEX self-energies on both clusters calculated at high $T$. In this regime, correlations are short ranged in nature and thus well described by the small cluster itself, while remaining long-ranged features, which are provided by the large cluster FLEX, are insignificant. The interpolated small cluster self-energy accurately replicates that of the explicit large single cluster QMC result. This results in a vanishing FLEX contribution within the Ansatz as the large and interpolated small cluster FLEX results are identical and thus cancel each other (see superimposed, lower set of curves in Fig. 3.7).

Figure 3.8: Flow chart depicting two independent self-consistent DCA calculations combined via an Ansatz to construct a MSMB self-energy.

In this high temperature regime (e.g. Fig. 3.7) the fully self-consistent Ansatz as well as our modified one remain numerically stable. However, one inherent limitation of the approach is already apparent. The observed magnitude of the negative imaginary part of the QMC self-energy is significantly smaller than the FLEX result. This overestimation of the self-energy by the FLEX deems a first order approximation to the vertex to be insufficient. A self-consistent implementation of the Ansatz aggregates the problem as the Ansatz self-energy used to initialize each FLEX iteration is similar in magnitude to the QMC self-energy. This results in an insufficient damping of the FLEX potentials and the subsequent overestimation of the FLEX self-energy renders the large cluster self-energy calculation numerically unstable. This is an inherent problem in the self-consistent approach. In an attempt to enhance the numeric stability of the MSMB method we remove the self-consistent implementation of the Ansatz on the large cluster. This leaves two independent DCA calculations for the small and large cluster which, after the individual problems are converged, are combined by the Ansatz. The resulting self-consistency scheme is depicted in Fig. 3.8. However, the effective media embedding the two cluster problems now are unaware of correlations as determined by the other cluster solver technique. Therefore, the effective medium of the large cluster now lacks the explicit short ranged correlations as provided by the QMC. Similarly, the effective medium of the small cluster only contains long-ranged correlations as provided by the dynamical mean-field approximation.

The third modification enters in the determination of the small cluster FLEX self-energy 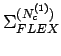$\Sigma _{FLEX}^{(N_c^{(1)})}$. Rather than calculating it explicitly, we obtain it by coarse graining the large cluster self-energy onto the small cluster. The combination of all changes introduced up to this point significantly increase the range of low temperatures which can be addressed by a perturbative MSMB approach.

Throughout the remainder of the paper we will restrict ourselves to the non-self-consistent momentum space Ansatz as outlined in this section. It indeed succeeds in addressing some of the problems encountered in the original implementation and yields a numerically stable MSMB method.