... interpolation ^3.1

We omit the additional coarse graining of the self-energy in the original work. This is deemed appropriate since the interpolated small cluster self-energy wont recoup the lattice self-energy and hence a coarse graining to a cluster is merit-less.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ^3.2

The DCA inherently has a lesser sign problem within the QMC compared to finite size approaches (2) and in the combination with a smaller cluster size results in a significantly larger average sign.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (B) ^4.1

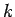The breathing mode actually can be properly defined only at the zone corner in 2D and at $k=\pi$ in 1D. However in this chapter we extend this nomenclature for all the $k$ points, even if this is not entirely correct.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... energy ^4.2

We set the lattice constant equal to unity.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... dispersion ^4.3

DOS for the linear dispersion is constant $= 1/v_F$ while for a 1D tight-binding dispersion it is infinite at $k=0$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

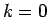... quasiparticle ^4.4

The physics at energies close to $\omega _0$ relative to Fermi surface is presumably not influenced much by the electron hole creation at the Fermi surface.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.