3.3 Approximations to the vertex

In this section we provide the remaining details of the $\lambda$-approximation. Previous studies, as well as our own results, have shown that in the positive $U$ Hubbard model the long-ranged contributions to the self-energy are dominated by the spin and charge fluctuations of the system. In contrast, pairing fluctuations are less significant and do not change the qualitative multi-scale results, unless very low temperatures are considered. The self-energy determination in the results section for the lowest order in $U$ approximation to $\Gamma^{\lambda}$ considers all three channels. However, the remaining higher order cases are restricted to only the self-energy contribution of the particle-hole channel. An equivalent derivation to the following can be trivially extended to the particle-particle channel.

Starting with the $\lambda$-approximation introduced in sections 3.2.2 (Eqs. 3.8 and 3.9), the Bethe-Salpeter equation (Eq. 3.7) for the approximated large cluster reducible vertex function can be coarse-grained to the small cluster (see section 3.6 for further details):

$$\begin{split}\overline{F}^\lambda(K_1,K'_1&,Q_2;\imath \omega... ...Q_2;\imath \omega_n'',\imath \omega_n', \imath \nu) \end{split}$$ (3.14)

where we coarse grained the bare particle-hole susceptibility bubble (internal legs in Fig. 3.4 which are lattice Green's functions). We call this coarse grained susceptibility $\overline{\chi}^0$

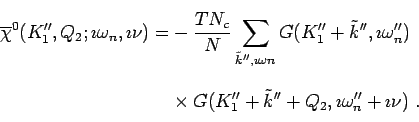$$\begin{split}\overline{\chi}^0(K''_1,Q_2;\imath \omega _n, \i... ...'_1+\tilde{k}''+Q_2,\imath \omega_n''+\imath \nu)~. \end{split}$$ (3.15)

Furthermore, while the coarse-graining (sum over internal moment $\tilde{k}''$) is to the small cluster, the self-energy in $G$ originates from the large cluster. The resulting reducible vertex function $\overline{F}^\lambda$ however, is still only defined for small cluster momenta but incorporates large cluster corrections from the coarse grained susceptibility $\overline{\chi}^0$. Due to these long-ranged contributions, the reducible vertex constructed in this manner is not equivalent to a QMC evaluated small cluster $F$.

The resulting Bethe-Salpeter equation (3.14) is most easily solved for $\overline{F}^\lambda$ in the following matrix form

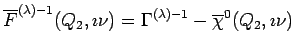$$\overline{F}^{(\lambda) -1}(Q_2,\imath \nu)=\Gamma^{(\lambda)-1}-\overline \chi^{0}(Q_2,\imath \nu)$$ (3.16)

where the matrix indices correspond to the internal momenta and frequency.

At this point, the self-energies can now finally be evaluated using the Dyson equation as illustrated in Fig. 3.3. On the large cluster this yields:

$$\begin{split}&\Sigma^{(N_c^{(2)})}_{\lambda}(K_2,\imath \omeg... ...\imath \omega_n',\imath \omega_n, \imath \nu)-U )~. \end{split}$$ (3.17)

Here we interpolate the small cluster momentum $M(K_2)\rightarrow K_2$ (for details see section 3.6) and subtracted $U$ in the parenthesis to prevent an over counting of the second order term.

In the calculation of the transverse spin fluctuation part, recall that $2\chi^{\pm} = \chi^{zz}$ where we define $\chi^\pm$ as the correlation function of $\sigma^+$ and $\sigma^-$, and $\chi^{zz}$ as the correlation function formed from $\sigma^z$. Then as $\chi^{zz} = 2(\chi^{\uparrow\uparrow} - \chi^{\downarrow\uparrow})$, we have that $\chi^\pm = \chi^{\uparrow\uparrow} - \chi^{\downarrow\uparrow}$ and $F^\pm=F^{\uparrow\uparrow} - F^{\downarrow\uparrow}$. This means that for the self-energy on the large cluster,

$$\begin{split}&\Sigma^{(N_c^{(2)})}_{\lambda}(K_2,\imath \omeg... ...ne{\chi}^0(K'_1,Q_2;\imath \omega_n', \imath \nu)~. \end{split}$$ (3.18)

While for the real-space implementation of the Ansatz, knowledge of the large cluster self-energy in the $\lambda$-approximation is sufficient, the momentum-space version requires the corresponding self-energy diagrams on the small cluster as well. An equivalent calculation on the small cluster yields for the self-energy in $\lambda$-approximation

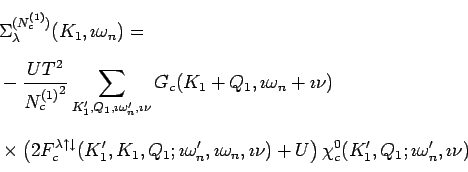$$\begin{split}&\Sigma^{(N_c^{(1)})}_{\lambda}(K_1,\imath \omeg... ...)\chi^0_{c}(K'_1,Q_1;\imath \omega _n', \imath \nu) \end{split}$$ (3.19)

where all single-particle propagators have been replaced by $G_c$, including the ones entering the bare bubble $\chi^0$.

We want to reiterate that the $\lambda$-approximated self energy thus obtained, is only accurate for long-ranged correlations. In order to obtain a viable multi-scale solution, the neglected short-ranged correlations have to be accounted for by means of the Ansatz, as outlined in the previous section.