3.3.1 First Order in $U$

The introduced non-perturbative MSMB method requires a detailed knowledge of the small (QMC) cluster irreducible vertex. This evaluation of $\Gamma$ however, poses a difficult and numerically involved problem. We shall therefore initially only consider perturbative approximations to the vertex within the MSMB method. In approximating the irreducible vertex by the frequency independent first order contribution i.e. $\Gamma(K,K';i\omega_n,i\omega_n')=U$, the self-energy diagrams of Fig. 3.3 reduce to the well known FLEX(16,17,18) diagrams. In the particle-hole channel, the corresponding self-energy is given by

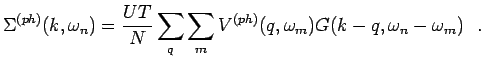$$\Sigma^{(ph)}(k,\omega_n)=\frac{U T}{N}\sum_q \sum_m V^{(ph)}(q,\omega_m) G(k-q,\omega_n-\omega_m)~~.$$ (3.20)

The FLEX potential is defined by

$$\begin{split}V^{(ph)} &=\chi^0_{ph}(q,\omega_n)-\frac{1}{2} \... ..._{ph}^{0~2}(q,\omega_n)}{1-\chi^0_{ph}(q,\omega_n)} \end{split}$$ (3.21)

where

$$\chi^0_{ph}(q,\omega_n)=-\frac{T}{N} \sum _{k} \sum_{\omega} G(k,\omega_m)G(k+q,\omega_m+\omega_n)~.$$ (3.22)

Using the FLEX to address the long length-scale problem within a multi-scale method was the scope of the work by J. Hague(3). Initially we will return to this simple cluster solver which is known to provide qualitatively correct long length-scale properties. We will use the FLEX to illustrate some of the properties and problems associated with the Ansatz in momentum space (see Eqs. 3.12 and 3.13). After exploring some of the encountered limitations, we will introduce variations of the original implementation which expand the scope of FLEX applicability within the MSMB scheme.