At lower temperature or for larger ![]() , higher-order terms in the
vertex are important. The second order corrections to the irreducible
vertex function in the
, higher-order terms in the
vertex are important. The second order corrections to the irreducible
vertex function in the ![]() -approximation (i.e. zero external
momentum transfer
-approximation (i.e. zero external
momentum transfer ![]() and frequency
and frequency ![]() ) are shown in
Fig. 3.6. The irreducible vertex is given in the spin
channel by
) are shown in
Fig. 3.6. The irreducible vertex is given in the spin
channel by
![\includegraphics[width=0.9\textwidth,clip, clip]{2ndorderU.eps}](img298.png) |
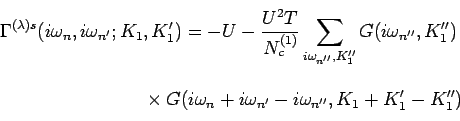 |
(3.23) |
and in the charge channel
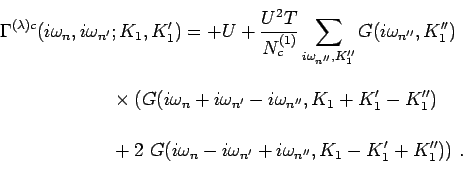 |
(3.24) |