Research and Interests
Solid State
Over the years substantial research has been done on trying to understand high temperature superconductivity. The study of correlated electron system has proved successful on various levels in this pursuit. The one-dimensional Hubbard model is one of the simplest ways of modeling correlated electron systems, reducing the complexity of the problem by only maintaining fermionic degrees of freedom and limiting the Coulomb repulsion to local interaction. Furthermore, the presence of Luttinger liquid(LL) behavior in the Hubbard model along with the proposition that high temperature superconductors should be considered Luttinger liquids gives yet further incentive to investigate this model.
One-dimensional systems, such as the one we intend to investigate have been subject to rigorous investigation due to the variety of experimental settings. Carbon nanotubes and various biological molecular conductors are just a couple of these systems exhibiting one-dimensional behavior.
 Most recently I have been developing a multi-scale extension to quantum cluster methods for strongly
correlated electron systems. This approach incorporates both long and short
scale physics alike thereby providing a fuller picture of the underlying
physics involved. Within this multi-scale extension correlations are approximated on any given
length-scale commensurate with the strength of the correlations on the respective scale. The shortest
length-scale are thus treated explicitly while longest ones are addressed at a mean-field level. In the
intermediate length-regime correlations are assumed to be weak and are approximated diagrammatically
based on the explicit knowledge of short-ranged two-particle correlation functions.
This multi-scale method constitutes a universally applicable extension to the well established cluster techniques and
provides results in very good quantitative agreement with substantially more expensive explicit methods such as Quantum Monte Carlo.
Most recently I have been developing a multi-scale extension to quantum cluster methods for strongly
correlated electron systems. This approach incorporates both long and short
scale physics alike thereby providing a fuller picture of the underlying
physics involved. Within this multi-scale extension correlations are approximated on any given
length-scale commensurate with the strength of the correlations on the respective scale. The shortest
length-scale are thus treated explicitly while longest ones are addressed at a mean-field level. In the
intermediate length-regime correlations are assumed to be weak and are approximated diagrammatically
based on the explicit knowledge of short-ranged two-particle correlation functions.
This multi-scale method constitutes a universally applicable extension to the well established cluster techniques and
provides results in very good quantitative agreement with substantially more expensive explicit methods such as Quantum Monte Carlo.
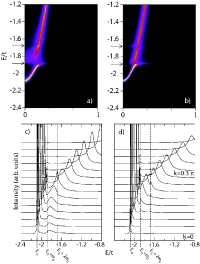 In a parallel project we explored the spectral properties of various polaron models in their
dependence on the type of electron-phonon coupling involved. These spectral properties of electron-phonon coupled systems
has become a field of increasing interest, especially
after angle-resolved photoemission (ARPES) experiments in cuprate superconductors revealed a kink in
the quasiparticle dispersion at an energy characteristic to a specific optical phonon mode. The
undoubtedly strong dependence on the electron-phonon interaction of the models still leaves many open opportunities for further investigation.
In a parallel project we explored the spectral properties of various polaron models in their
dependence on the type of electron-phonon coupling involved. These spectral properties of electron-phonon coupled systems
has become a field of increasing interest, especially
after angle-resolved photoemission (ARPES) experiments in cuprate superconductors revealed a kink in
the quasiparticle dispersion at an energy characteristic to a specific optical phonon mode. The
undoubtedly strong dependence on the electron-phonon interaction of the models still leaves many open opportunities for further investigation.
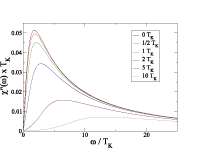 The initial project of my graduate studies was the development of a semi-analytical solution of the
Kondo model in a magnetic field. We have shown that the single impurity Kondo model at zero temperature in a magnetic
field can be solved by a semi-analytical approach based on the Wegner flow equation method. The resulting problem is shown
to be equivalent to a resonant level model with a non-constant hybridization function. Within this nontrivial effective
hybridization function all necessary quasiparticle interactions in the Kondo limit are translated into a the simple non-interacting Anderson model, thus providing a simple way of obtaining various thermodynamic quantities and the
dynamical spin-structure factors.
The initial project of my graduate studies was the development of a semi-analytical solution of the
Kondo model in a magnetic field. We have shown that the single impurity Kondo model at zero temperature in a magnetic
field can be solved by a semi-analytical approach based on the Wegner flow equation method. The resulting problem is shown
to be equivalent to a resonant level model with a non-constant hybridization function. Within this nontrivial effective
hybridization function all necessary quasiparticle interactions in the Kondo limit are translated into a the simple non-interacting Anderson model, thus providing a simple way of obtaining various thermodynamic quantities and the
dynamical spin-structure factors.
Education:
My current education research focuses on the effectiveness of secondary implementations of proven curricula and methods. A move towards web-based instruction with the aim of promoting student comprehension has been pushed for some time. Conceptual gains have been found in implementations substituting computer simulations in place of real laboratory equipment, augmenting lecture components via web-based multimedia pre-lectures, or Just in Time Teaching implementations. However many other proven pedagogical tools have not been implemented online and their effectiveness in this medium remains questionable. Tutorials in Introductory Physics is one such research-based curriculum which has been adopted by many institutions in an attempt to improve first year introductory calculus based physics courses. Students working through the workbook in small collaborative learning groups have been shown to significantly better develop conceptual understanding and scientific reasoning skills than those in traditional recitations.